독학으로 대학 수학을 공부한 문과생이 수학의 장점을 알려본다

수학을 어려워하시나요? 수식을 보면 두드러기가 난다? 라는 수학을 연상하는 것만으로도 알레르기가 생기는 분들에게 수학의 장점을 문과적 관점에서 이야기할 수 있었으면 좋겠습니다!!! ٩(๑❛ᴗ❛๑)۶

↓ 저에 대한 것
수학 경력 : 대략 2년 (2021/06 ~ 2023/03 (기사 작성 당시))
이공계 학생이라면 배울만한 수학 분야는 대략적으로 학습해했음 :
1. 해석학
2. 대수학
3. 기하학

잘하는 순서
해석학(확률 통계 > 미적분학) > 대수학(선형대수) > 기하학(집합, 위상공간론)
수학을 시작한 이유 : 데이터 사이언티스트에게 필요한 기술 중 하나였기 때문입니다.

아래는 이 글을 만드는데 활용했습니다 (*ﾟ∀ﾟ*)

독학으로 대학 수학을 공부한 문과생이 수학의 장점을 알려본다

이 글의 작성 이유
1. 수학이 어렵다는 가치관을 바꾸고 싶다
수학을 통해 배운 것 & 수학을 배움으로써 얻을 수 있는 이점
마지막으로
추천 수학 유튜브 채널
참고 문헌

이 글의 작성 이유

수학이 어렵다는 가치관을 바꾸고 싶다

어렵다고 생각하면 어려운 것으로 해석하고, 그 어려운 것에서 멀어지게 됩니다. 수학이 어렵다고 생각하면 강제적인 환경의 영향을 제외하고는 수학 관련 내용을 스스로 학습하지 않을 것 같습니다. 그 어려워하는 것은 수학에만 한정된 이야기가 아닙니다.

이 글에서는 여러분들의 그런 해석(사고)을 바꿀 수 있었으면 좋겠습니다.
해석(생각)을 바꾸면 그 한 대상에 대한 감정과 행동도 바뀝니다.
또한 수학이 다양한 ‘깨달음’과 ‘사물을 보는 관점’을 준다는 것을 느낄 수 있을 것입니다.

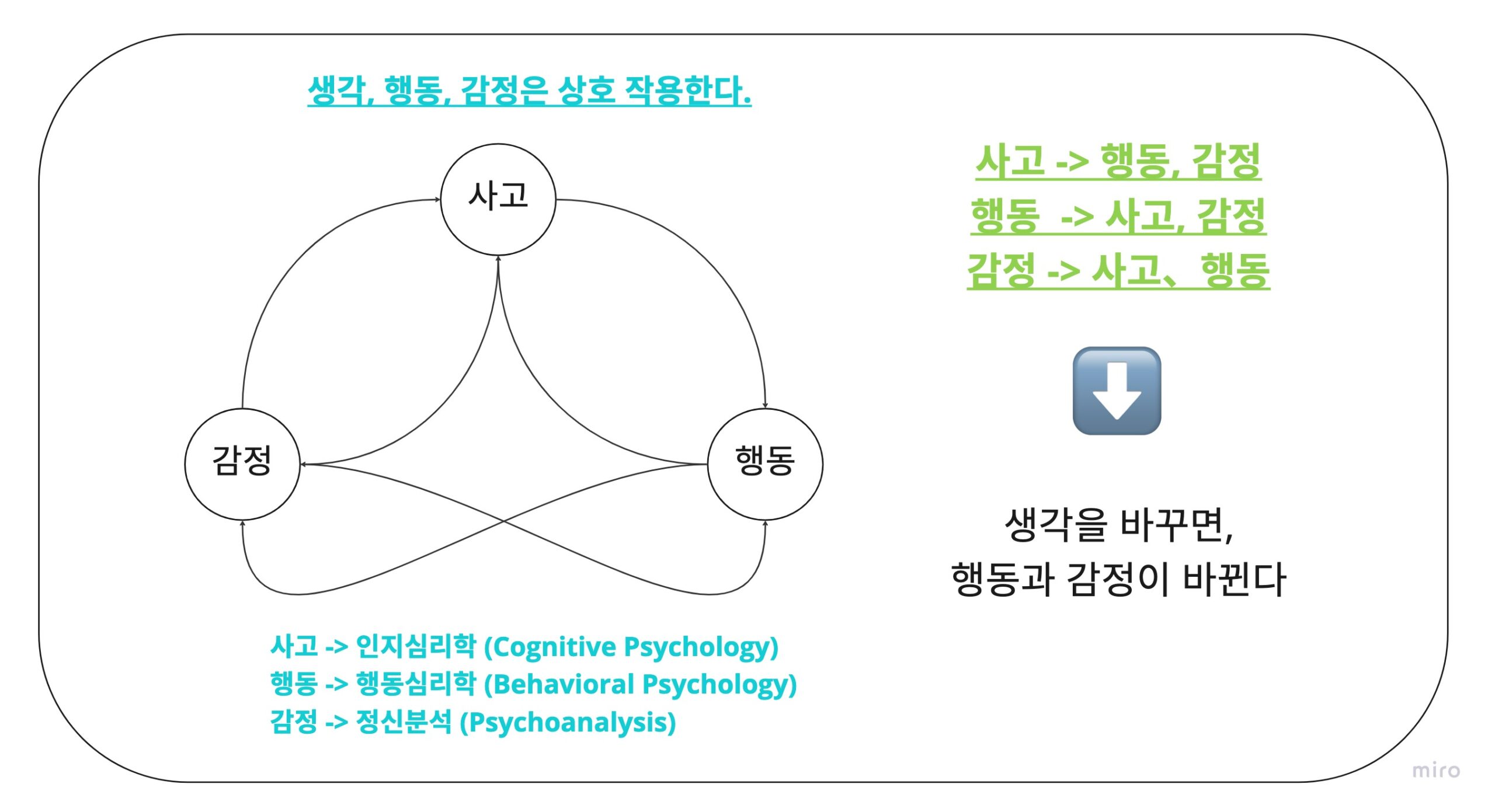
수학을 통해 배운 것 & 수학을 배움으로써 얻을 수 있는 이점

수학에서 배운 것 -> 전제의 중요성

전제가 다르면 결과(결론)도 달라진다.

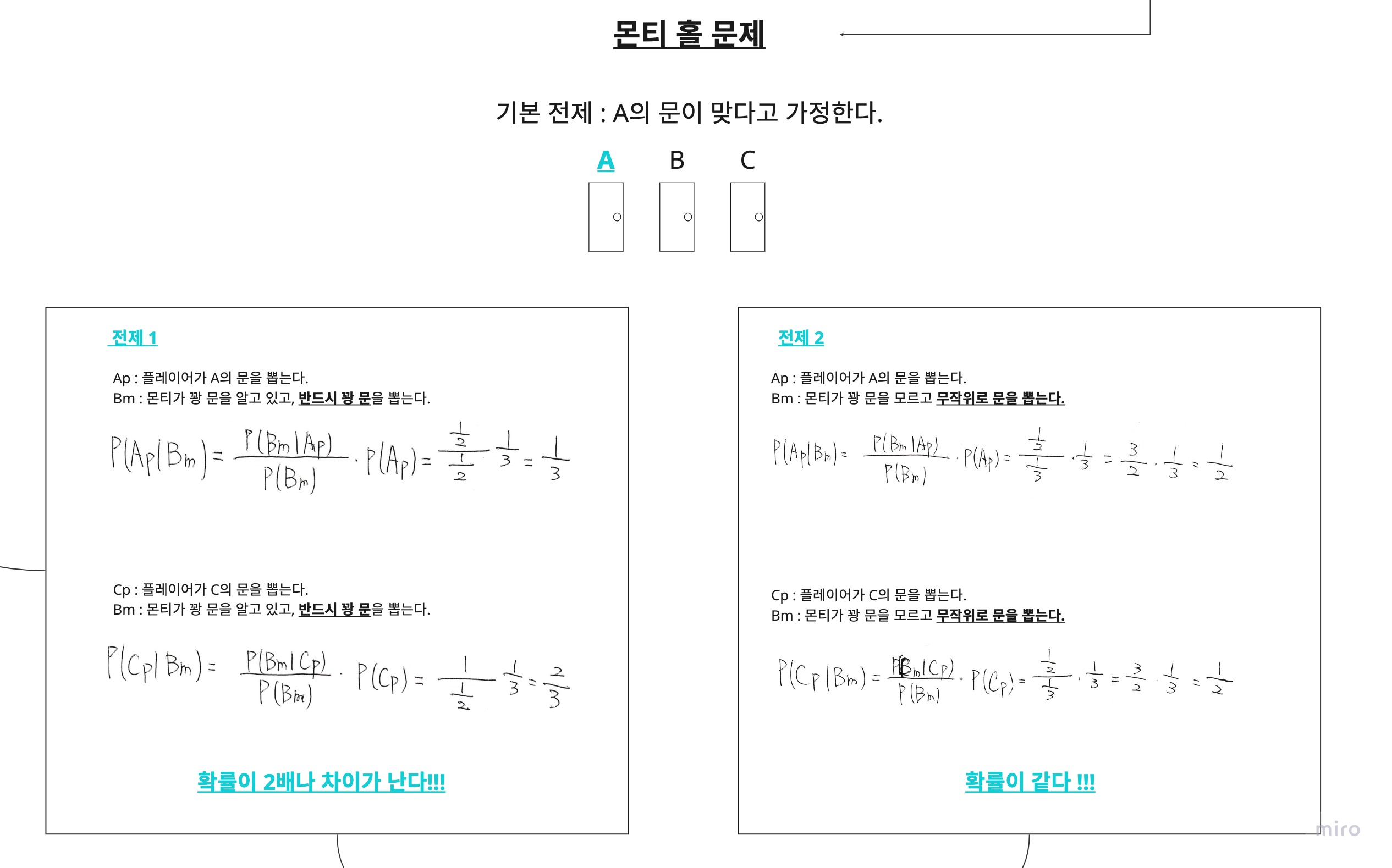
몬티 홀 문제

<게시된 상담>
플레이어 앞에 닫힌 3개의 문이 있고, 1개의 문 뒤에는 경품인 새 차가 있고, 2개의 문 뒤에는 당첨을 의미하는 염소가 있다. 플레이어는 새 차의 문을 맞추면 새 차를 받을 수 있다. 플레이어가 하나의 문을 선택하면 사회자 몬티가 나머지 문 중 염소가 있는 문을 열어 염소를 보여준다.

여기서 플레이어는 처음 선택한 문을 나머지 열려있지 않은 문으로 바꿀 수 있다고 한다. 여기서 플레이어는 문을 바꿔야 할까?

1990년 9월 9일 발행된 뉴스잡지 ‘Parade’에서 마릴린 보스 사반트가 연재하는 칼럼 ‘마릴린에게 맡겨라’에서 위의 독자 투고 질문에 “정답은 ‘문을 바꾸어라’이다. 왜냐하면 문을 바꾸면 경품을 받을 확률이 2배가 되기 때문이다”라고 답했다. 그러자 곧바로 독자들로부터 “그녀의 답은 틀렸다”는 투서가 약 1만 건에 달했고, 이 문제는 큰 논란으로 발전했다.

출처: 무료 백과사전 ‘위키피디아(Wikipedia)

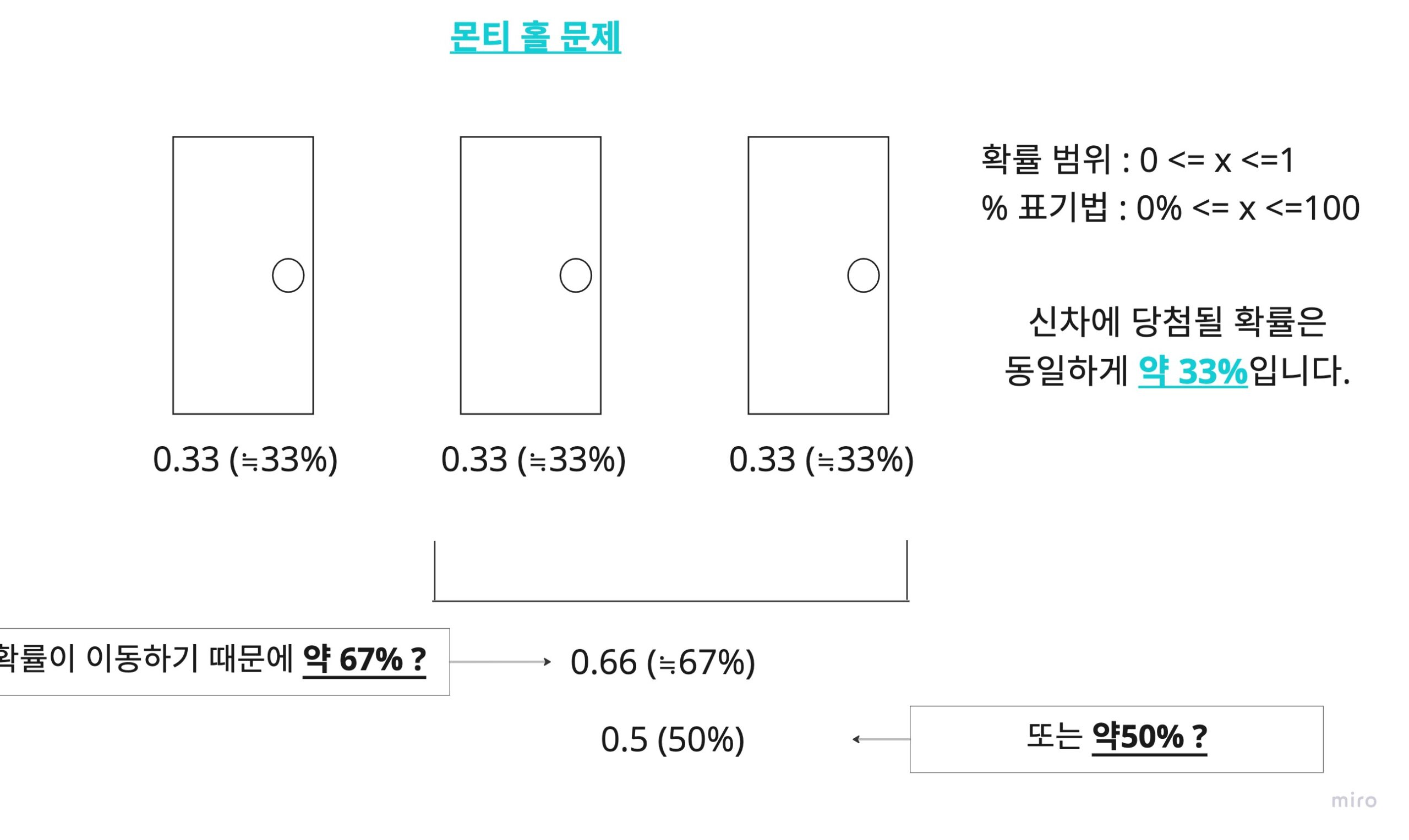
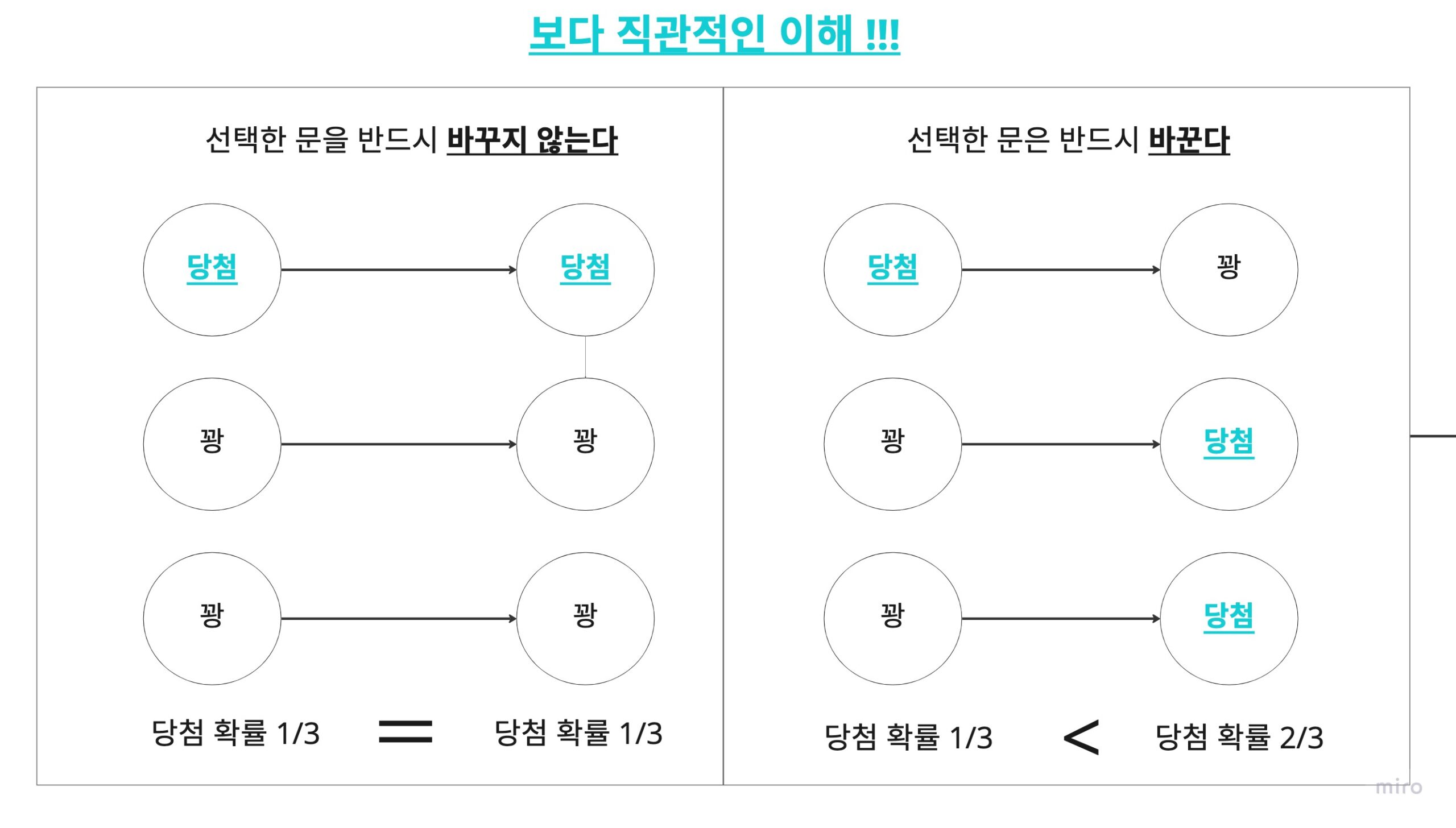
↑위와 같은 결과가 나오기 위해서는 어떤 전제가 있었을까?
베이즈 정리를 통해 생각해 보자
( 도망가지 마세요~!
한 번 보시기 바랍니다 (°▽°) )

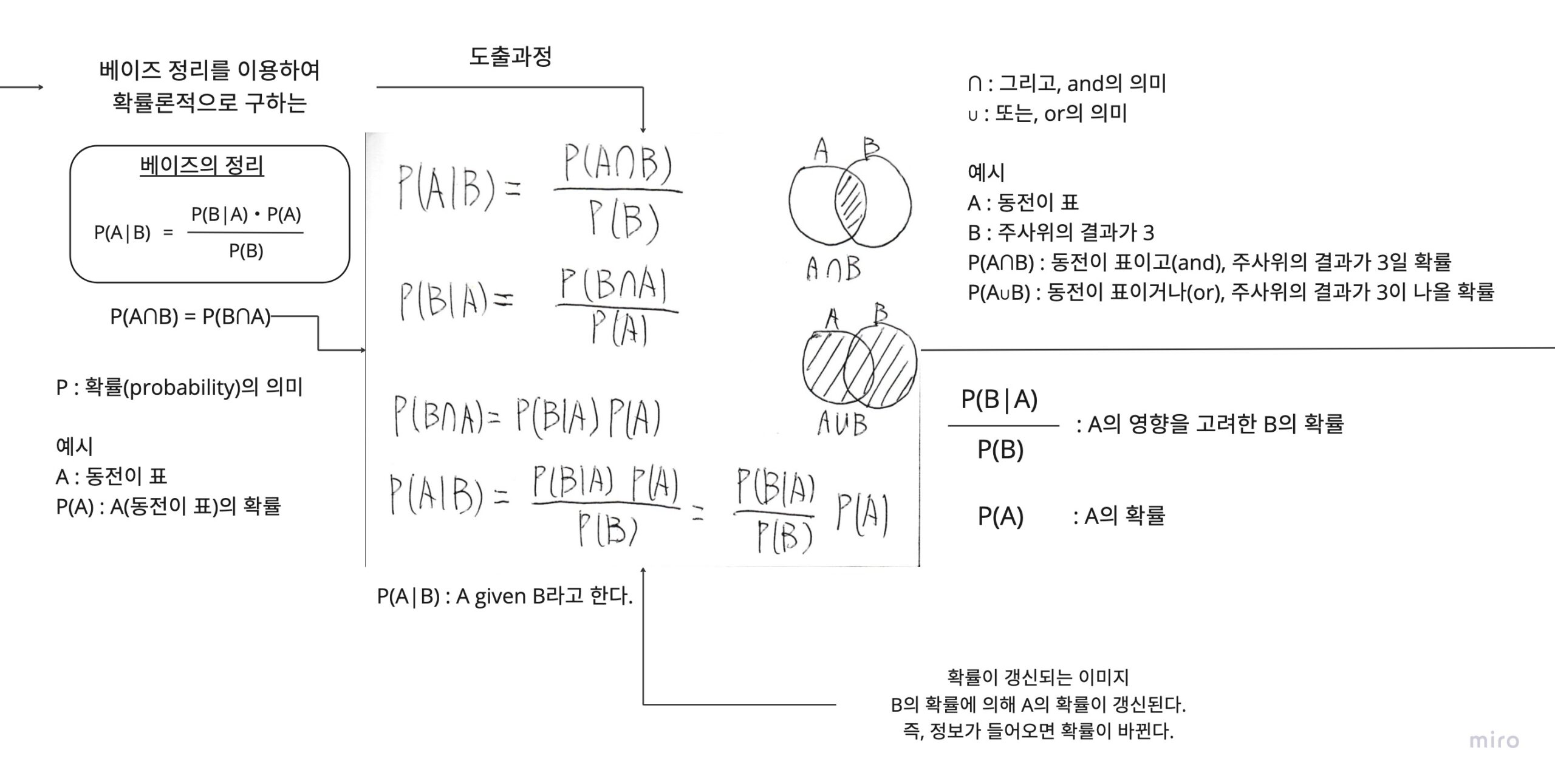
↓이것은 생략하셔도 됩니다 !!!

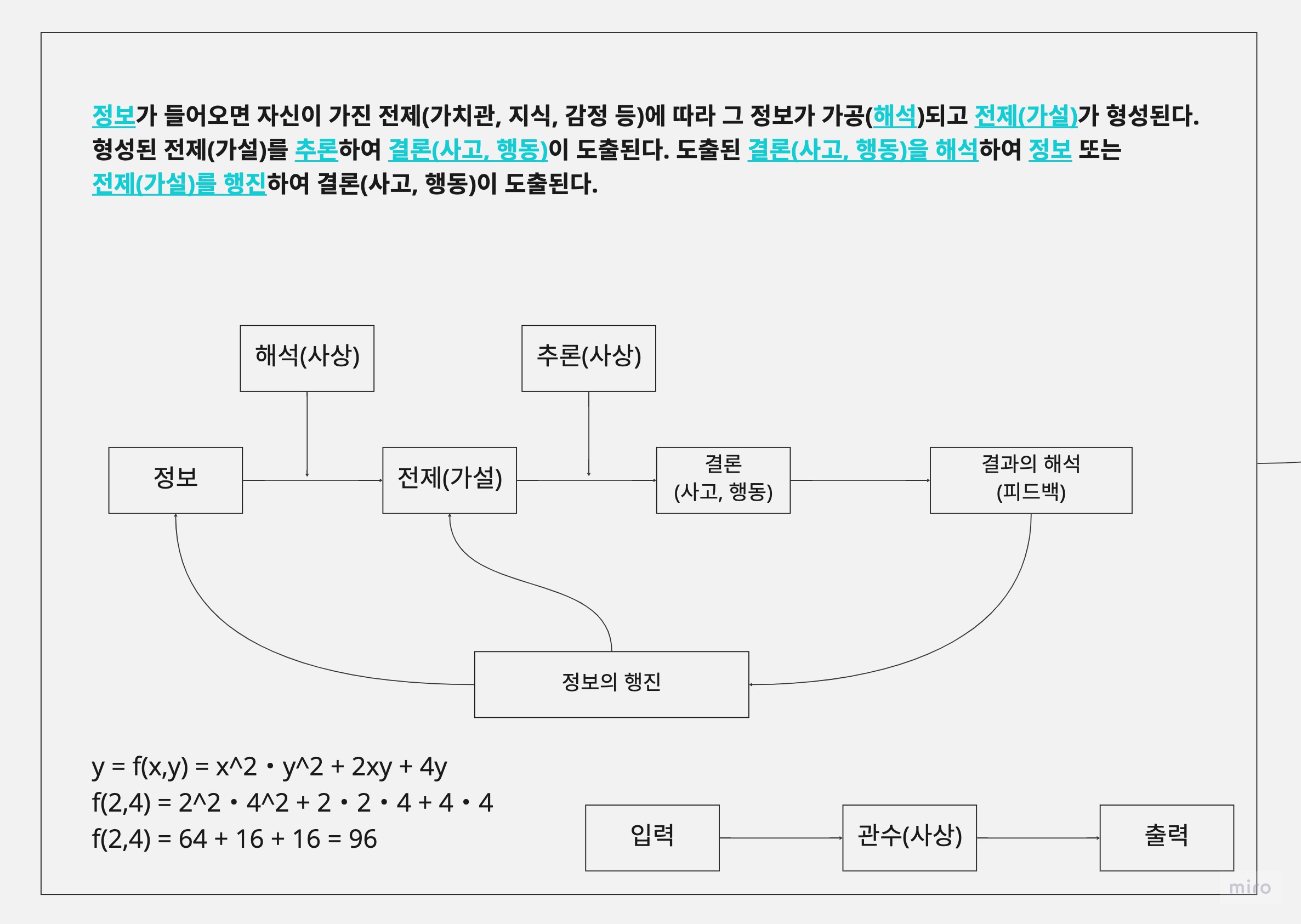
수학을 배움으로써 얻을 수 있는 이점 -> 생각에 논리성을 부여해준다.

논리적이고, 확률적으로 생각할 수 있게 됩니다.

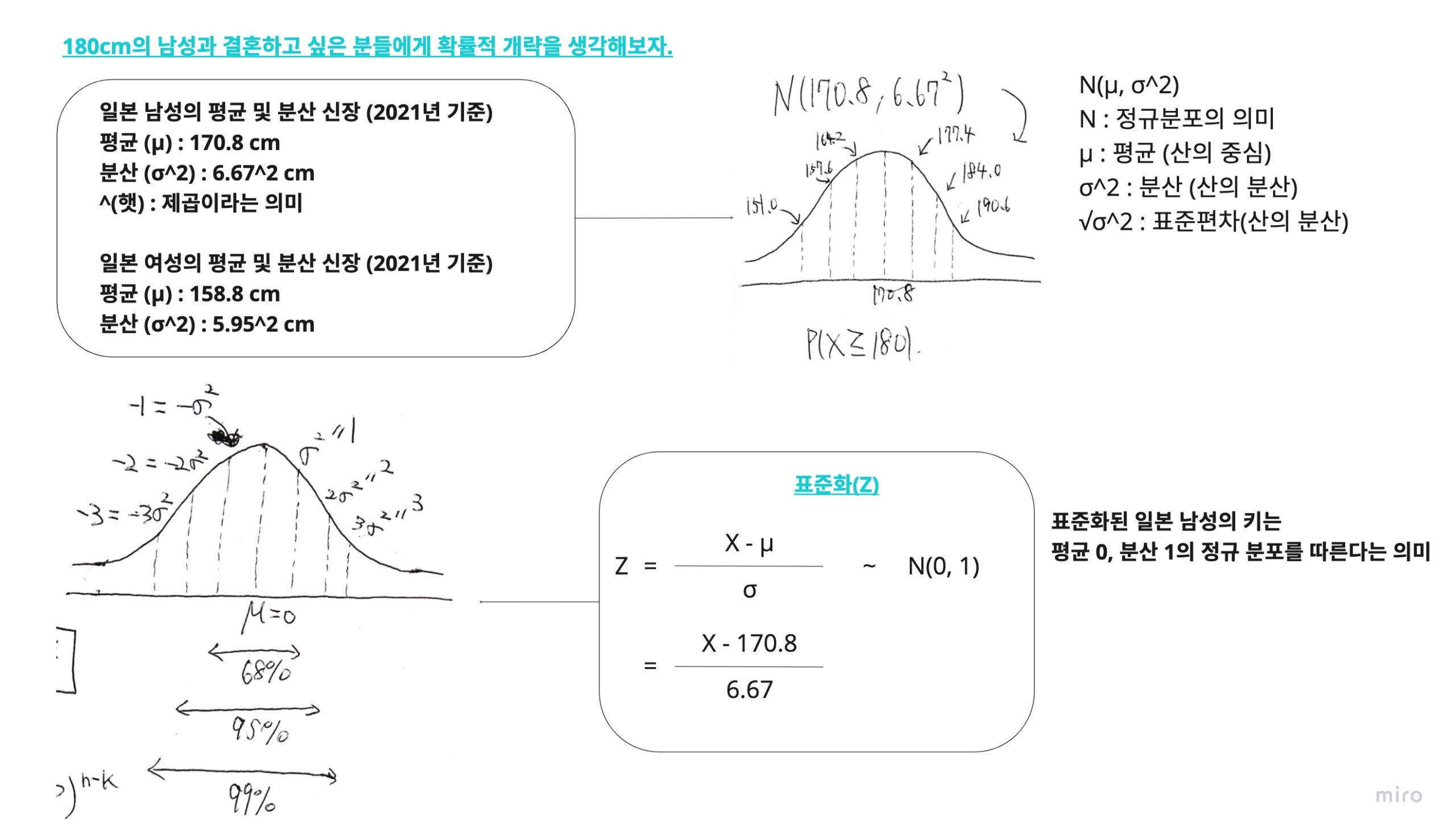
예를 들어, 180cm의 남자와 결혼하고 싶은 분에게 확률적인 개략적인 계산을 생각해 본다.

소셜게임에서 레어 캐릭터를 맞출 확률을 구한다.

이 당첨 확률은 네이피어 수에 따라 결정됩니다.
이 설명은 아래 추천 수학 유튜브 채널에 있습니다,
관심이 생기면 시청해 보세요 ( ・∇・)

마지막으로

수학은 당연한 것을 말하고 있다

수학은 두렵지 않고 누구나 할 수 있다고 저는 생각합니다. 여러분은 수학을 어렵게 생각하실 수도 있습니다. 실제로 수학은 어려운 것이 있습니다. 하지만 수학은 지극히 평범한 것을 말하는 경우가 많습니다. 자연 현상이나 당연한 것을 표현하려고 하면 수학이 적합했던 것 같아요.

그래서 자연 현상이나 당연한 것을 어떻게 숫자로 표현할 것인가, 그 자체를 찾는 학문이 수학이라고 저는 그렇게 생각합니다. 즉, 철학입니다. 철학에 숫자가 들어간 것이 수학이라는 것이죠. 우리가 평소에 생각하는 것들에 수의 개념이 들어가면 그것은 수학이 됩니다.

예를 들어 확률론으로 생각하면 주사위의 눈은 1~6까지 있기 때문에 한 번 주사위를 굴리면 어떤 결과가 나올 확률은 1/6이 됩니다. 이것은 정상적인 것이라고 생각합니다. 하지만 이것은 왜곡된 주사위가 아니라는 전제가 필요합니다. 이 결과를 도출하기 위한 다른 전제가 있을 수 있지만, 직관적으로도 이해할 수 있을 것 같습니다.

기호를 읽을 수 있으면 언젠가는 이해하고 활용할 수 있게 된다.

수학에서 중요한 것은 무엇을 하는지 이해하는 것입니다. 즉, 수식(문자)을 읽을 수 있게 되면 일단은 처음은 좋습니다. 언어학 같은 것을 생각해보면 이해가 되실 텐데요, 영어를 제2외국어로 배울 때 일반적으로 문자를 먼저 배우게 됩니다. 이것은 영어뿐만 아니라 한국어, 중국어, 스페인어, 프랑스어 등도 마찬가지라고 생각합니다.

제2외국어로 글자부터 배우는 이유는 단순히 읽을 수 있어야 이해할 수 있기 때문입니다.
물론 소리만 외우는 맹자도 있겠지만, 일반적으로는 글자를 외우고 그 글자와 소리를 연결하는 것을 반복하면서 그 글자에 의미를 부여하고 이해, 암기하는 것입니다.

수학도 마찬가지로 수학의 기호에도 고유의 소리와 의미가 있습니다.
예를 들어

Σ -> 시그마

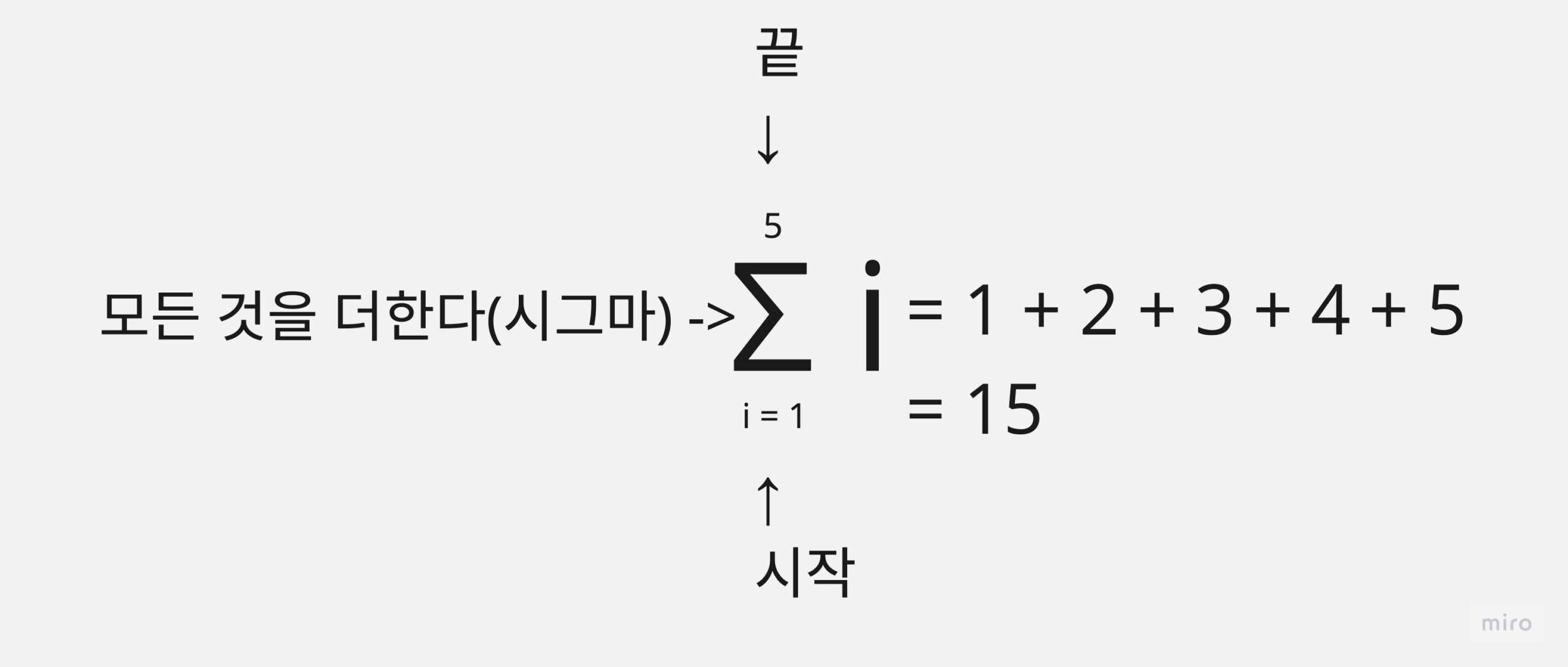
ε -> 엡실론

읽을 수 있으면 언젠가는 반드시 이해할 수 있습니다. 이해하면 반복 학습으로 사용할 수 있게 됩니다.
학습은 기본적으로 이 반복입니다.

뭘부터 배워야 할까?

수학에는 다음과 같은 분야가 있습니다.

미분, 적분을 연구하는 해석학 (lim, ∮ 등)
숫자를 문자로 바꾸어 방정식을 푸는 방법을 연구하는 대수학 (i, N, Z)
도형의 성질을 연구하는 기하학(π, sin, cos, tan 등)

수학의 어느 분야도 독립적이지 않고 서로 밀접한 관련이 있습니다.

개인적으로 추천하는 것은 확률통계학(해석학)입니다. 왜냐하면 일상 생활에서 확률의 개념은 적용하기 쉽기 때문입니다. 예를 들어, poker나 splender, colonist와 같은 게임에서 복권이나 한국인의 평균 소득 통계 등을 읽어내거나 미래 예측도 어느 정도 할 수 있게 됩니다.