数学が苦手? 数式を見たら蕁麻疹が出る? という数学を連想するだけでアレルギーが出てしまう方に数学の良さを文系の視点から語っていけたらと思います !!! ٩(๑❛ᴗ❛๑)۶
↓私について
数学歴 : 大体2年 (2021/06 ~ 2023/03 (記事作成当時))
理系学生であれば学ぶであろう数学の分野は大体学習した :
1. 解析学
2. 代数学
3. 幾何学
得意順
解析学(確率統計 > 微積) > 代数学(線形代数) > 幾何学(集合、位相空間論)
数学を学び始めた理由 : データサイエンティストに必要なスキルセットの1つだったから
以下が関連の記事になります。ご興味があれば読んでみてください(Youtubeに動画を投稿しました!)
以下はこの記事を作るのに活用したものです (*゚∀゚*)
この記事の作成理由
数学が難しいとする価値観を変えたい
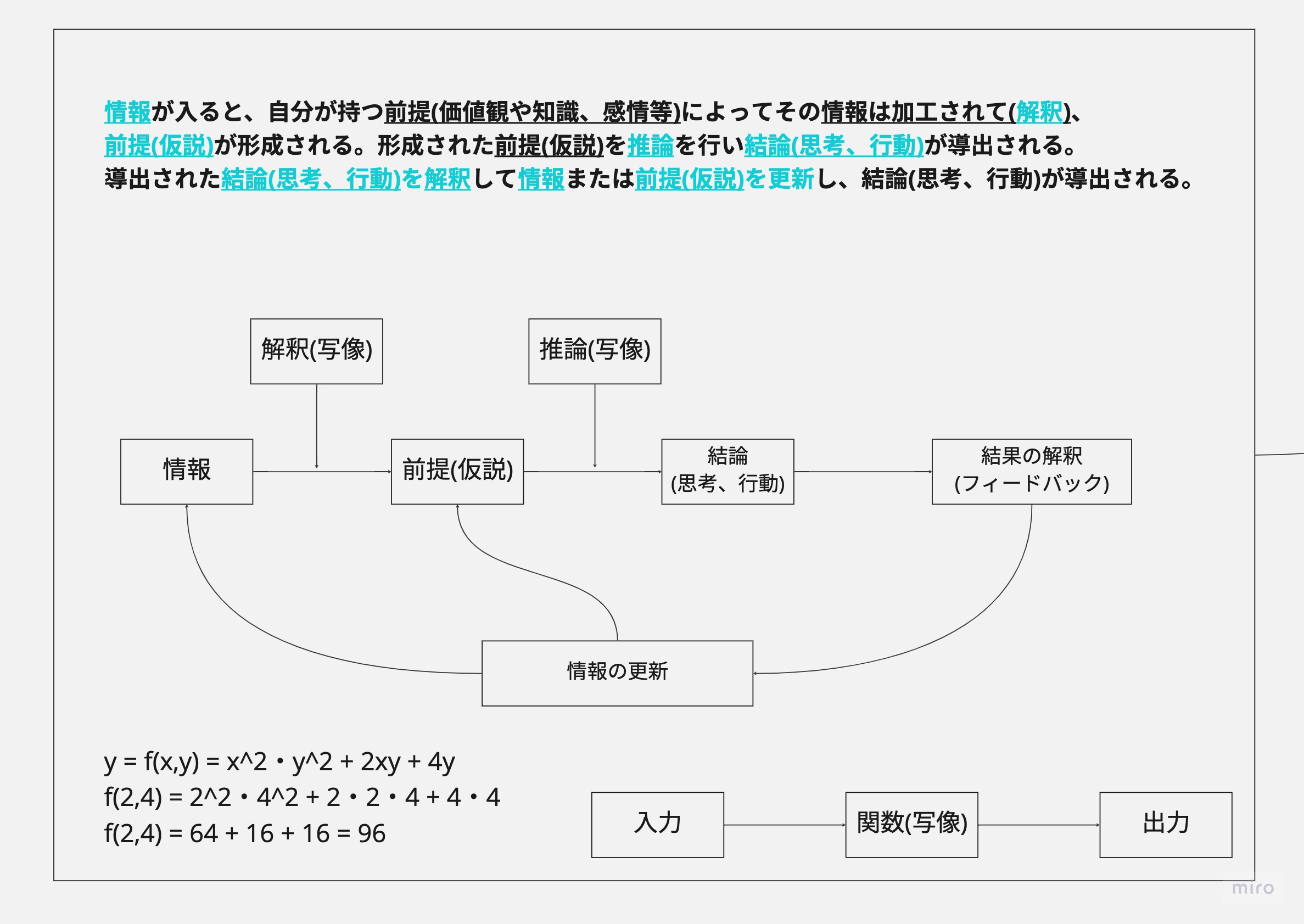
難しいと思ったら、難しいものだと解釈して、その難しいものから遠ざかっていきます。数学が難しいと思ったら、強制力のある環境の影響を除いては、数学関連の内容を自分から学習することはないと思います。その苦手なことは数学だけに限った話ではありません。
この記事では皆さんのその解釈(思考)を変えていけたらと思います。
解釈(思考)を変えることで、その苦手な対象に対しての感情と行動も変わります。
また数学がいろいろな “気づき” や “ 物を見る観点 ” を与えてくれることを実感するはずです。
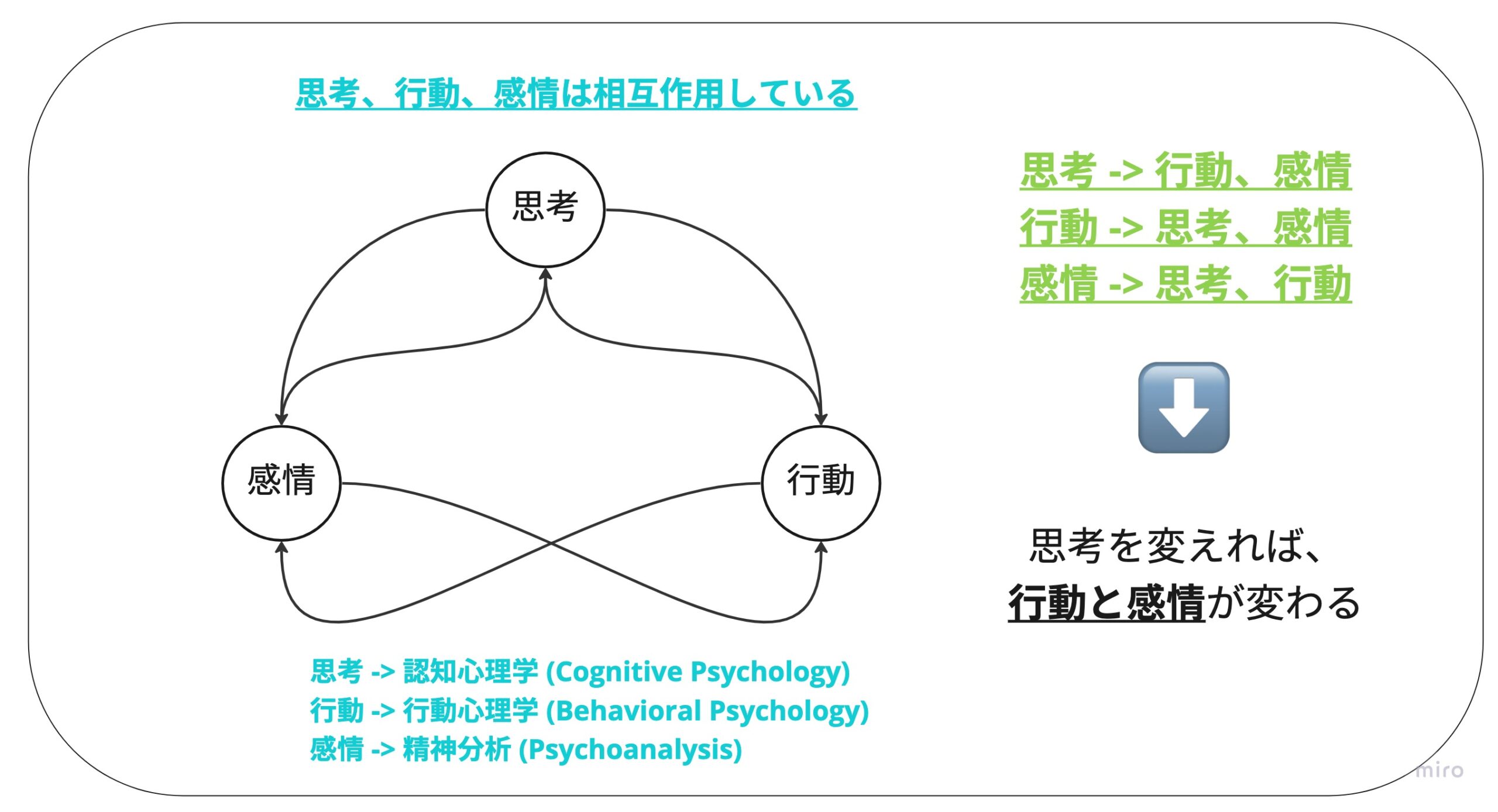
数学から学んだこと & 数学を学ぶことによる利点
数学から学んだこと -> 前提の重要性
前提が違えば、結果(結論)も変わる
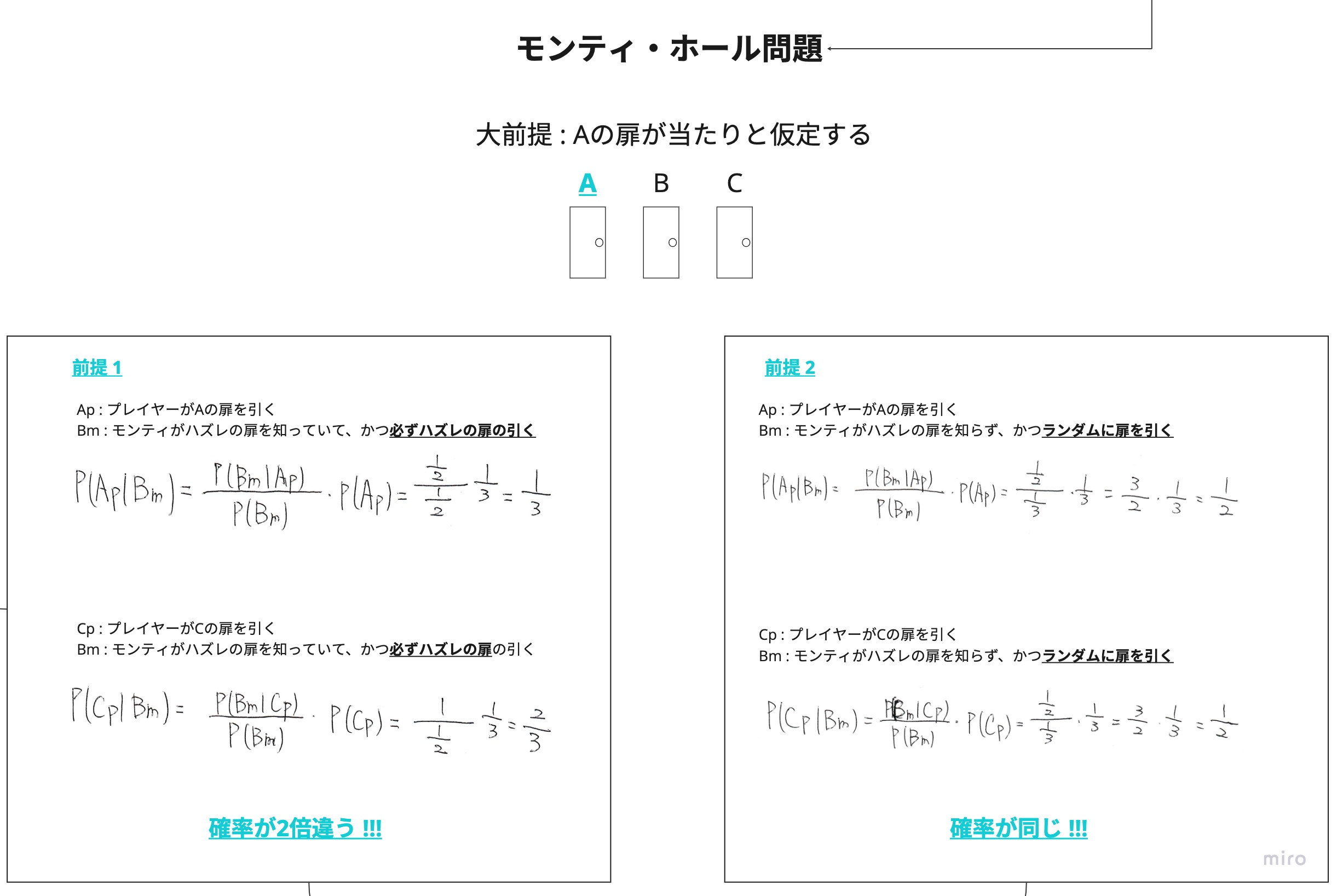
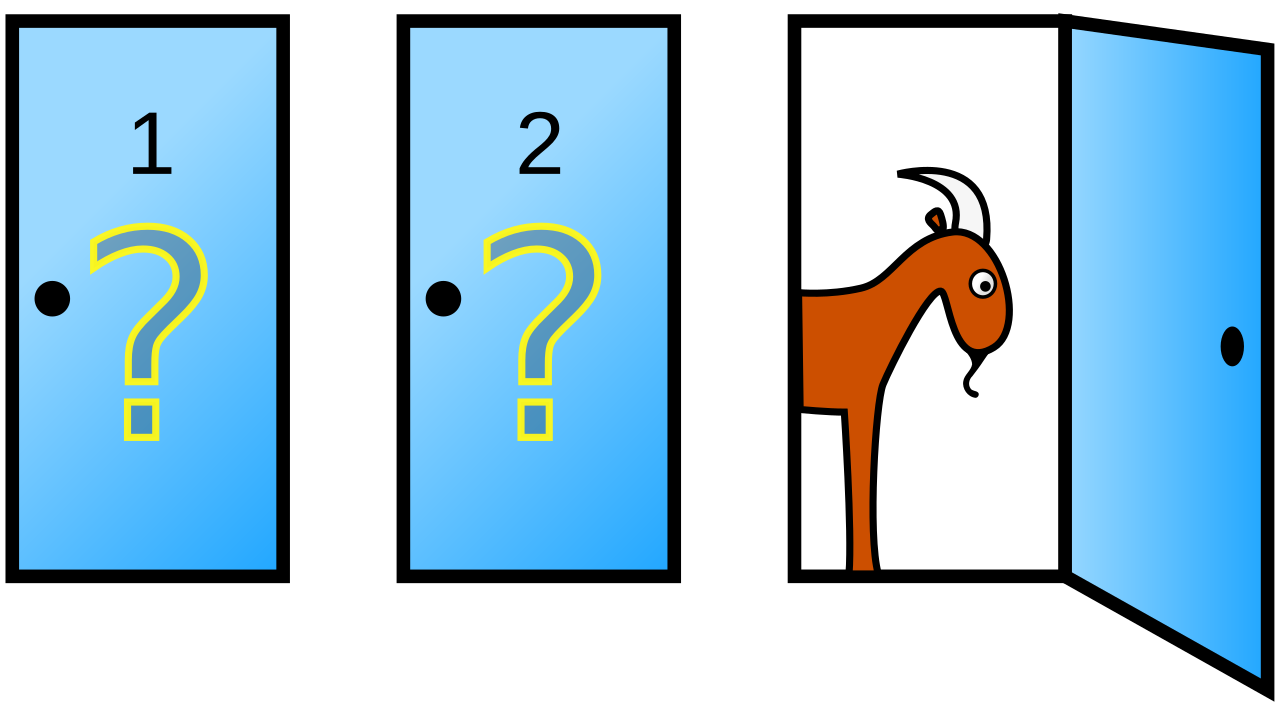
モンティ・ホール問題
<投稿された相談>
プレーヤーの前に閉じた3つのドアがあって、1つのドアの後ろには景品の新車が、2つのドアの後ろには、はずれを意味するヤギがいる。プレーヤーは新車のドアを当てると新車がもらえる。プレーヤーが1つのドアを選択した後、司会のモンティが残りのドアのうちヤギがいるドアを開けてヤギを見せる。ここでプレーヤーは、最初に選んだドアを、残っている開けられていないドアに変更してもよいと言われる。ここでプレーヤーはドアを変更すべきだろうか?
1990年9月9日発行、ニュース雑誌「Parade」にてマリリン・ボス・サヴァントが連載するコラム「マリリンにおまかせ」で、上記の読者投稿による質問に「正解は『ドアを変更する』である。なぜなら、ドアを変更した場合には景品を当てる確率が2倍になるからだ」と回答。すると直後から、読者からの「彼女の解答は間違っている」との約1万通の投書が殺到し、本問題は大議論に発展した。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
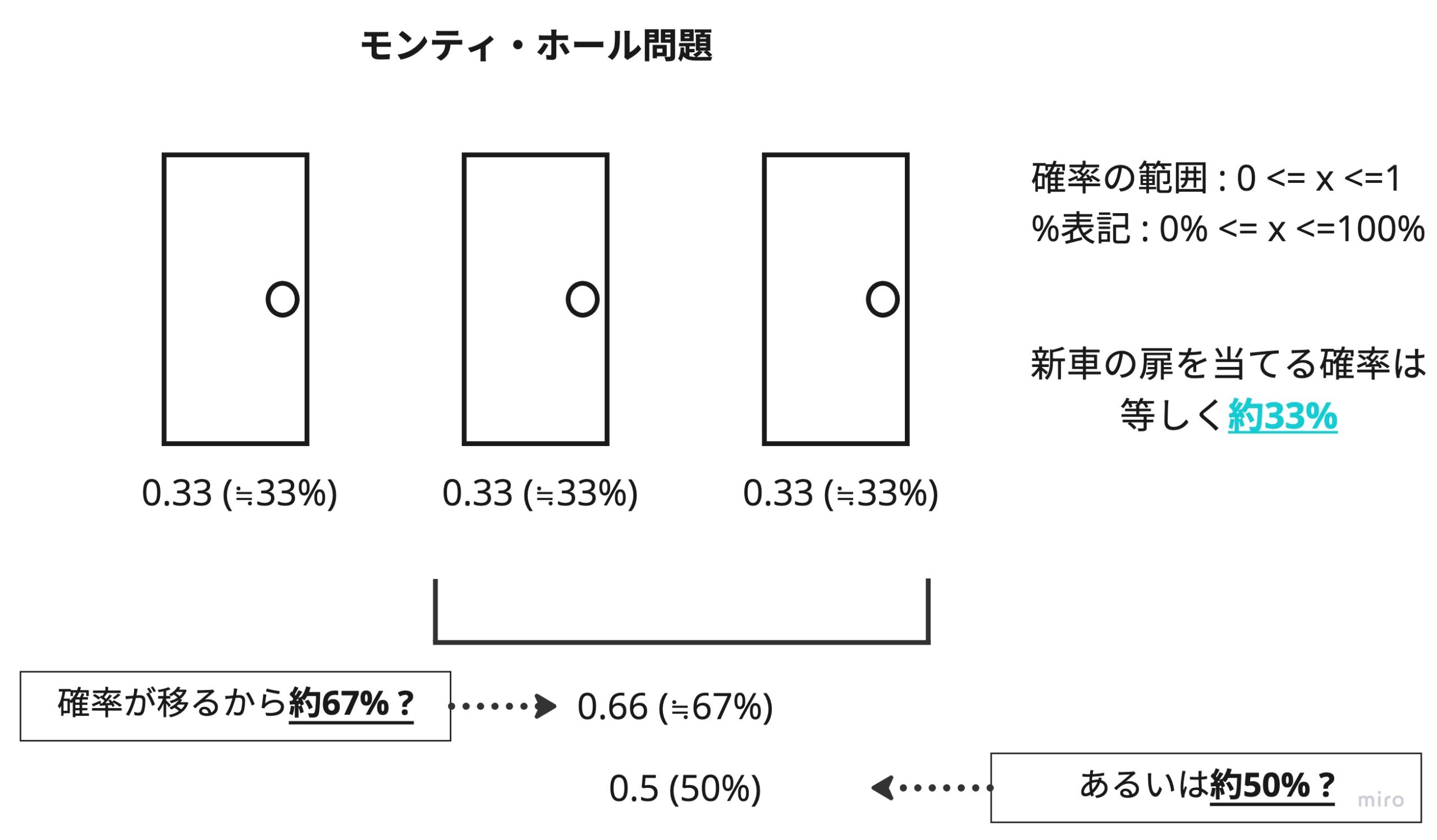
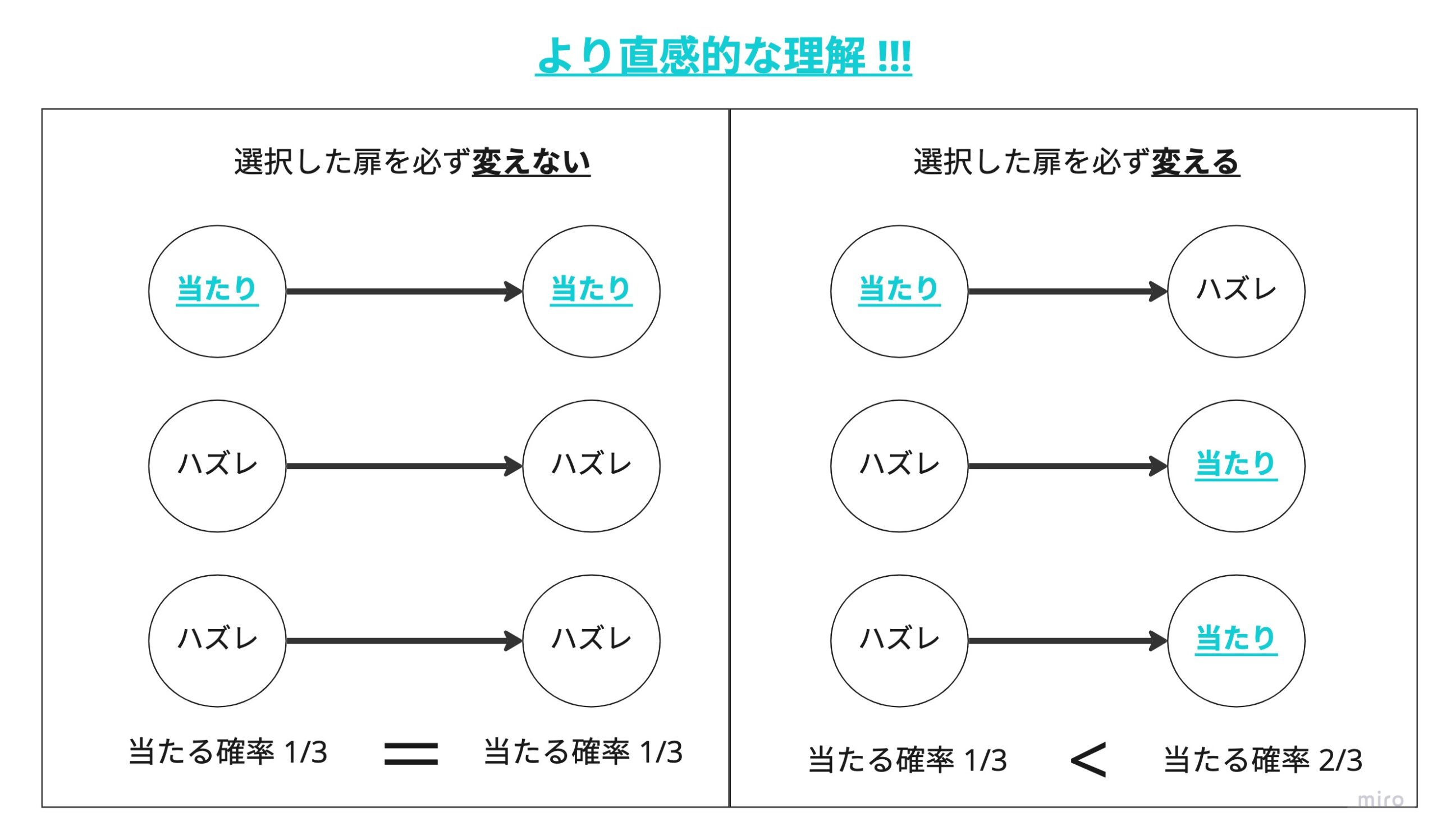
↑の結果が出るためにはどのような前提があったのか?
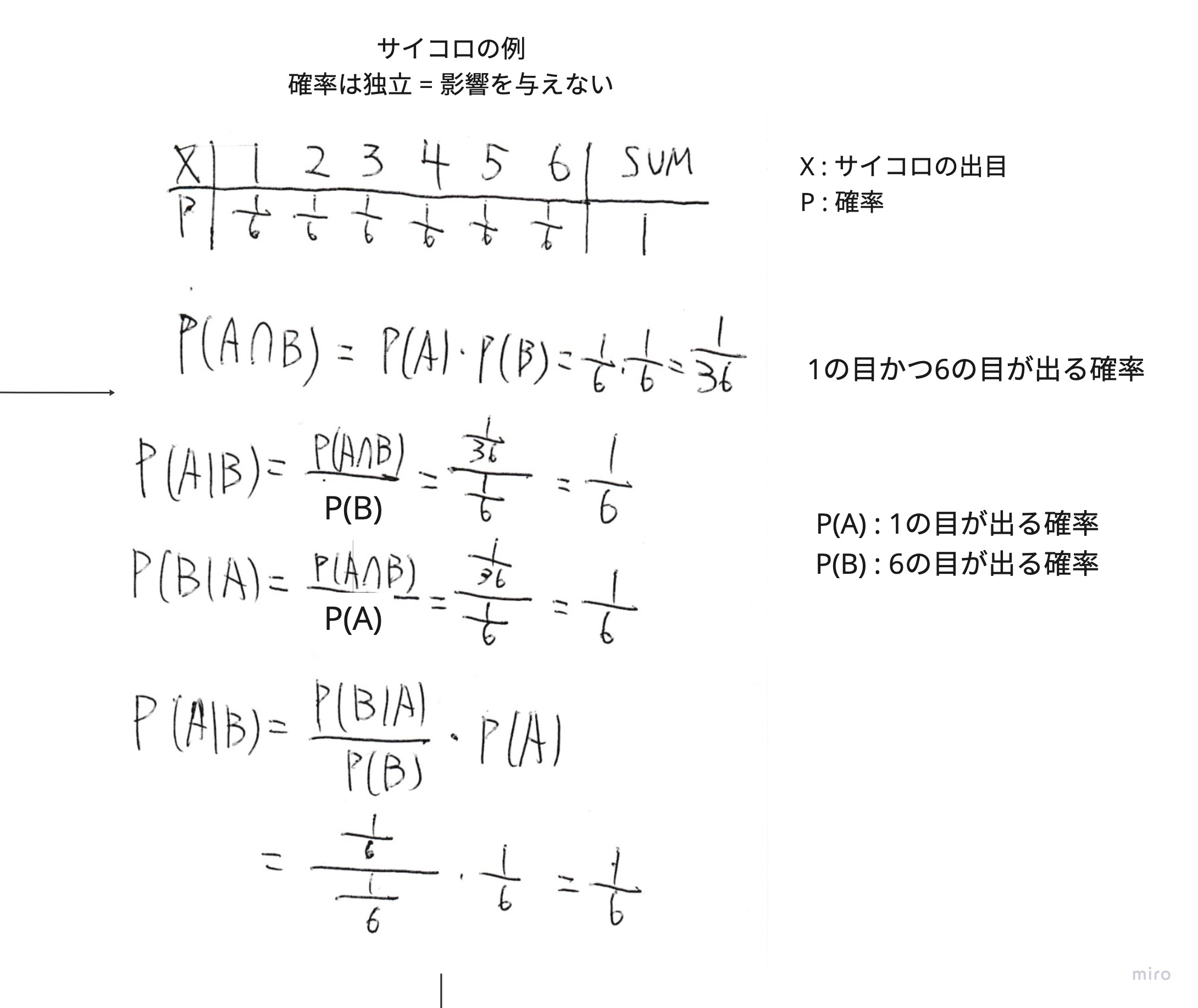
ベイズの定理を使って考えてみる
( 逃げないでください~
一回みてみてください (°▽°) )
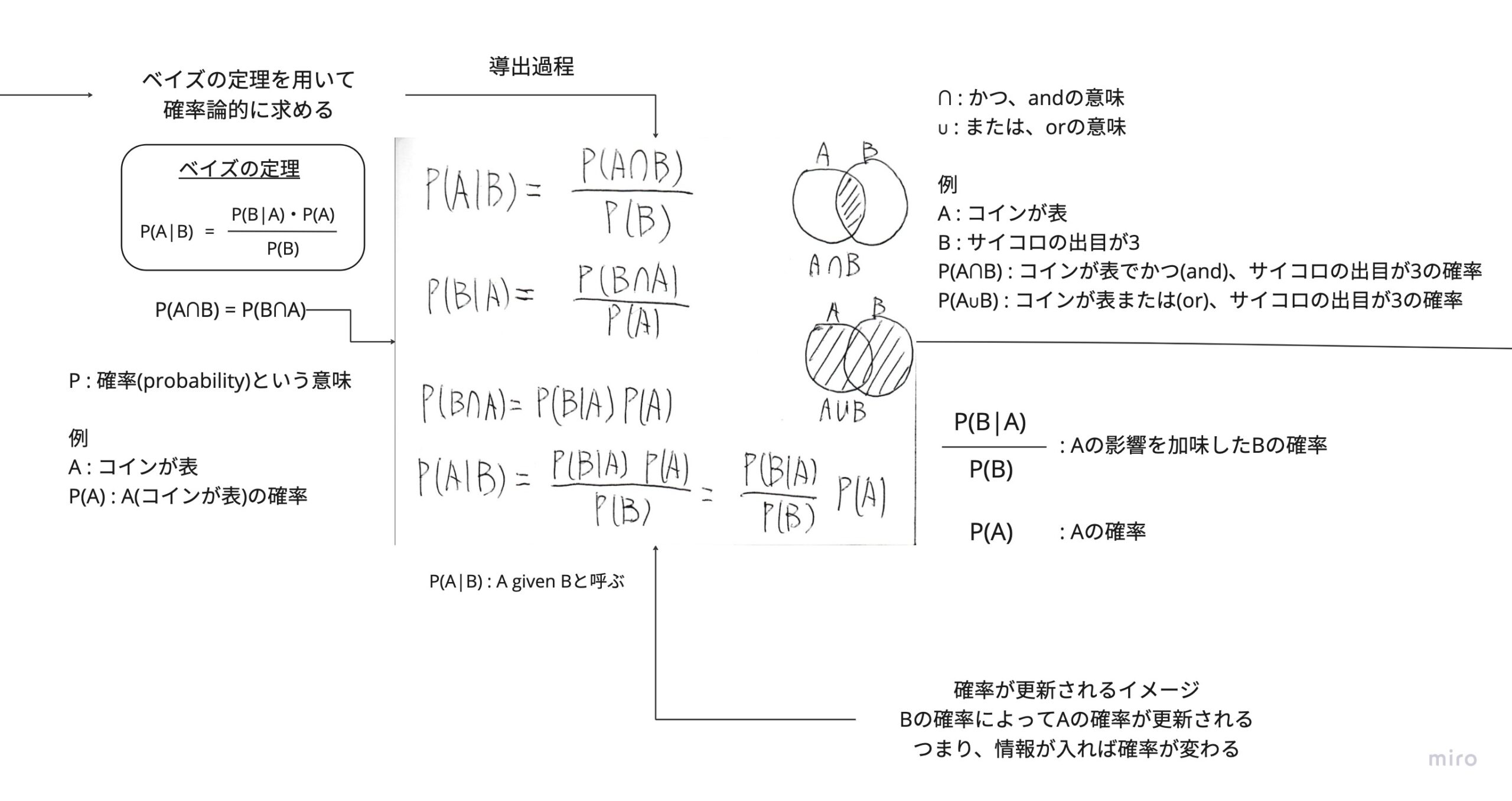
↓ここは飛ばしても良いです !!

数学を学ぶことによる利点 -> 思考に論理性を与えてくれる
論理的にかつ、確率的に考えることができるようになります。
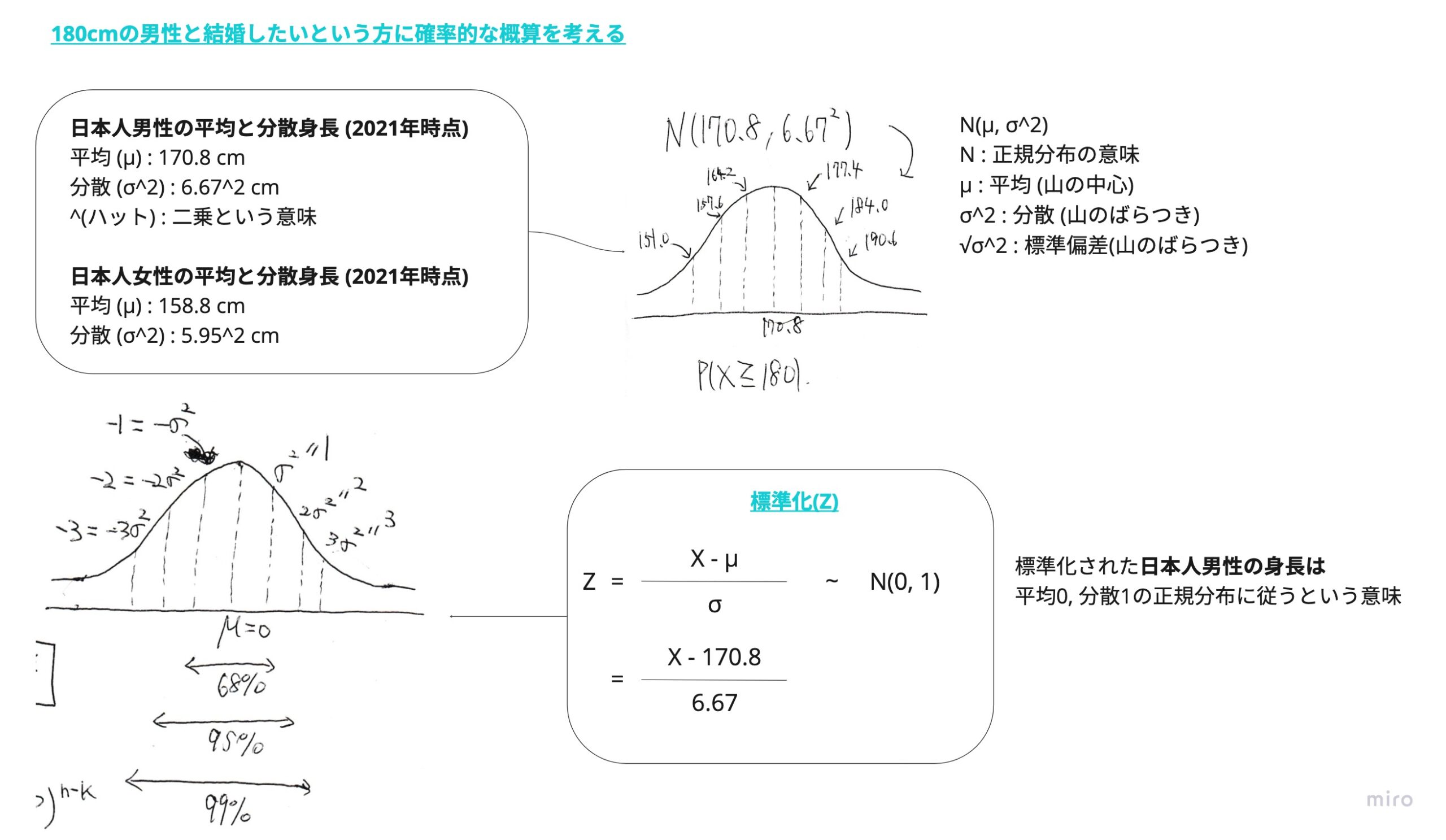
例えば、180cmの男性と結婚したいという方に確率的な概算を考える

ソーシャルゲームのレアキャラを当てる確率を求める

この当たる確率はネイピア数に従っています。
この説明は下のおすすめの数学Youtubeチャンネルにあるので、
ご興味が沸いたら、視聴してみてください ( ・∇・)
最後に
数学は当たり前を言っている
数学は怖くないし、誰でもできると私は考えています。皆さん数学を難しいと思っているかもしれません。実際数学は難しいものをあります。ですが、数学とは至極普通のことを言っていることが多いです。自然現象や当たり前のことを表現しようと思ったら数学が適していたみたいな感じです。
なので自然現象や当たり前のことをどう数で表現するのかやそれ自体を見つける学問が数学だと私はそう思っています。つまり哲学です。哲学に数が入ったのが数学ということになります。普段考えるようなことに数の概念が入ればそれは数学になります。
例えば、確率論で考えるとサイコロの出る目は1~6まであるので、一回サイコロを振ったら、ある出目が出る確率は1/6になります。これって普通のことだと思います。ですがこれは歪なサイコロでないことが前提に必要です。他にもこの結果を出すための前提があるかもしれませんが、直感でも理解できると思います。
記号が読めればいつか理解でき、活用できるようになる
数学で大事なのは何をしているか理解することです。つまり数式(文字)を読めるようになればとりあえず最初はそれで良いです。言語学なんかを考えてみればイメージがつくと思うのですが、英語を第二言語として学ぶときに一般的には文字を最初に学ぶと思います。これは英語に限らず、韓国語、中国語、スペイン語、フランス語なども同じだと思います。
第二言語として文字から学ぶ理由は単純に読めなきゃ理解できないからです。
もちろん音だけで暗記する猛者もいると思いますが、一般的には文字を覚えて、その文字と音を結びつけることの繰り返しをすることで、その文字に意味を付与して理解、記憶していきます。
数学も同じように数学に記号にもそれ独自の音と意味があります。
例えば
Σ -> シグマ
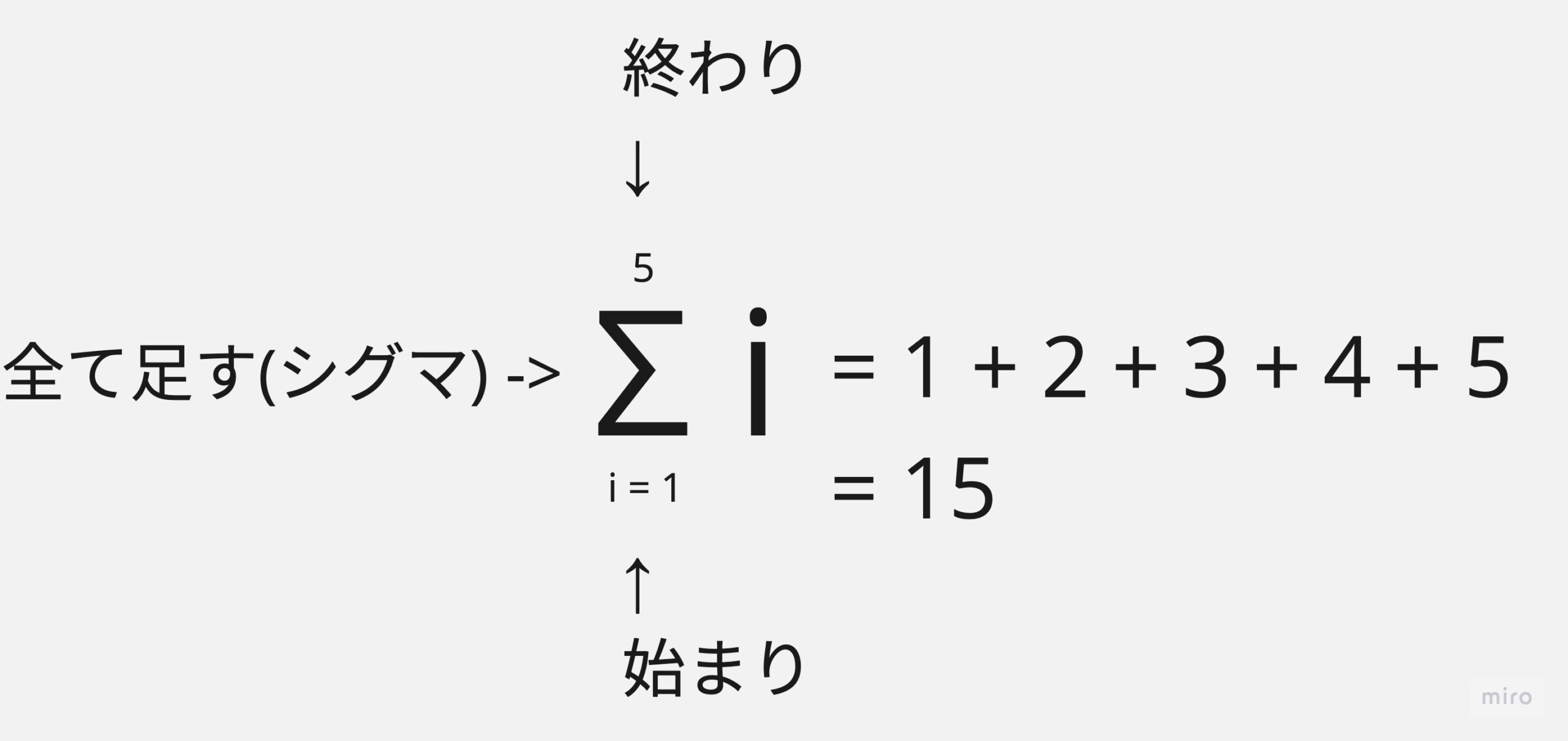
ε -> イプシロン

読めればいつか必ず理解できます。理解できれば反復学習で使えるようになります
学習は基本的にこの繰り返しです。
何から学べば良い?
数学には以下の分野があります。
微分・積分を研究する解析学 (lim, ∮とか)
数字を文字に置き換えて方程式の解き方を研究する代数学 (i, N, Z)
図形の性質を研究する幾何学(π, sin, cos, tanとか)
数学のどの分野も独立しておらずお互いに密接の関連があります。
個人的にお勧めするのは確率統計(解析学)です。なぜなら日常生活において確率の考え方は適用しやすいからです。例えば、pokerやsplender, colonistのようなゲームから宝くじや日本人の平均収入の統計等読み解いたり、将来の予測とかもある程度はできるようになります。
以下がわかりやすく数学を教えてくれています。
よくまとめられているので、この記事で興味を持っていただけたら、ご視聴してみてください (*゚∀゚*)
おすすめの数学Youtubeチャンネル
数学初級者
数学が世の中のいたるところで使われていることを実感できます Σ(‘◉⌓◉’)
数に親近感を持てるようになるはずです !!
数学中級者
数学をしっかり学ぶために基礎づくりです。
私のおすすめとして統計学を先に学ぶことをおすすすします。
一つ数学の得意な分野を作れば、他の数学を相互で関連があるので理解しやすくなるはずです!!
数学上級者
ここまで来れば、私から言うことはもうありません (°▽°)
数学ライフを楽しんでください !!
参考文献




Comment